«Параллель Тучкова». Часть пятая, в которой новые эксперты проводят новую экспертизу
Теперь, когда у нас есть необходимые теоретические знания из второй части и мы с вами вооружены необходимыми инструментами, которые я описал в части четвертой, давайте наконец приступим к новым измерениям и вычислениям!
Однако подождите. Я ведь вам еще не сказал, что собственно мы будем измерять. Как вы уже наверное догадались, лучшие инструменты потребуют и лучшего набора данных. И такой набор действительно есть. Уже много лет тому назад на сайте польского проекта mapywig.org были размещены прекрасные сканы военно-топографической трехверстной карты [1], которые не содержат тех неприятных дефектов, о которых я упоминал во второй части. Второй важной особенностью этих карт является то, что большинство из них может быть легко датировано, как минимум, по принципу «не ранее, чем...», а для значительного количества существует и точная датировка до года. Эти датировки я еще буду не раз обсуждать впоследствии, пока же отметим, что такая возможность есть.
Второй важный вопрос, который лучше всего задать с самого начала — это сколько измерений нам понадобится? В таблице, которую я сейчас начну обсуждать, приведено 160 измеренных углов (ровно столько, сколько было измерено в 2011-м году), однако это совершенно не значит, что для решения нашей задачи с приемлемыми точностью и надежностью необходимо такое количество. Более того, как мы с вами увидим немного позже, избыток измерений может быть так же вреден, как и их недостаток. Будем считать, что в таблицу я включил данные с запасом, для того, чтобы они были под рукой для других работ впоследствии.
Давайте теперь начнем вводить данные в таблицу, а заодно и посмотрим, как она устроена. Сейчас нас будут интересовать первые два листа: «Геометрия листов» и «Расчет по 3 меридианам». Первый лист, «Геометрия...» содержит необходимую описательную часть и исходные данные измерений, весь же нужный нам расчет ведется на втором листе. Рассчитываемые ячейки всех таблиц (те, которые содержат формулы или ссылки на другие ячейки) отмечены светло-серым цветом фона, те же ячейки, которые требуют ввода «сырых» данных, оставлены без заливки.
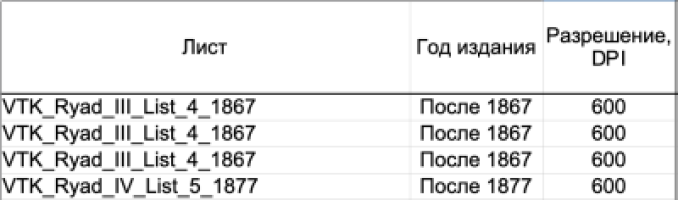
Самый первый столбец «Лист» содержит названия листов карт в том виде, в котором они хранятся на сайте Mapster. Все они содержат в названии фрагмент «VTK». Названия без этого фрагмента относятся к небольшому массиву платных сканов, о которых я писал во второй части, и которые я добавил к основному массиву большей частью для сравнения. Листы карт в целом упорядочены вначале по горизонтальным рядам с севера на юг, а внутри ряда — по вертикальным колоннам с запада на восток [2]. Если внутри одного листа удавалось измерить более одного угла, то и данные, относящиеся к этому листу упорядочены таким же образом: по уменьшению широты с севера на юг, а внутри одного значения широты — с запада на восток [3].
Следующий столбец «Год издания». Здесь я пошел по максимально консервативному пути: точно датированной (до года) считается карта, имеющая отпечатанную надпись с указанием года печати или составления, например: «Составлено в 1923 г. по рекогносцировке 1922 г.» или «Печатано в VI — 1909». Если же на листе карты указаны лишь даты уточняющих съемок или рекогносцировок, то такие листы я считаю окончательно составленными (а следовательно, и отпечатанными) не ранее или даже после соответствующего года съемки или рекогносцировки. Никакие другие пометки на карте, которые можно было бы принять за даты, в расчет не принимались. Возможно, что авторам некоторых карандашных пометок год издания и был очевиден из каких-то своих источников, но для нас с вами эти источники отсутствуют [4].
Столбец «Разрешение» показывает разрешение выбранного листа в пикселях растра на дюйм. Данные для него берутся из свойств выбранного изображения в редакторе GIMP. Эта величина позволяет пересчитать измерения, сделанные инструментом Измеритель GIMP из пикселей в дюймы. Прямо сейчас величины в дюймах нам не понадобятся, однако для справок и дальнейшей работы они включены в таблицу, о чем немного ниже.
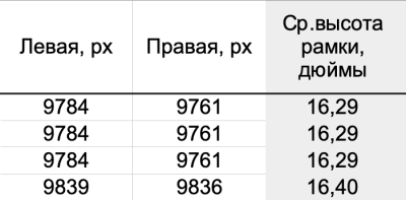
Следующие три столбца таблицы («Левая», «Правая» и «Ср. высота рамки») и относятся к вертикальным размерам внутренней границы рамки карты. Очевидным образом, средняя высота в дюймах получается простым усреднением левой и правой границ с последующим пересчетом, используя данные о разрешении. Угол наклона вертикальных границ рамки относительно границ растра я тут не использую, поскольку эти величины справочные.
Зато этот угол мы с вами учтем при измерении горизонтальных границ рамки (это следующие 9 столбцов). Измеряя инструментом GIMP, к примеру, верхнюю границу, мы сразу имеем три величины: «ширину» (горизонтальный катет прямоугольного треугольника), «высоту» (вертикальный катет) и угол в градусах («угол верхней изм., град»). Этот угол и есть угол наклона листа карты относительно границ растра, который, как мы помним из предыдущей части, обязательно следует учесть после измерения наклона хорды, стягивающей два меридиана. Точно такие же измерения сделаем и для нижней границы, а в дальнейших вычислениях оба этих угла усредним. Так же, как и абзацем выше, «Средняя ширина рамки» в дюймах получится из этих двух измерений. Что же касается оставшихся двух столбцов в этой группе (с «рассчитанными» углами) и которые, в отличие от «измеренных», я даю с точностью до трех знаков после запятой, то они рассчитываются по простой тригонометрической формуле из величин измеренных катетов и, как уже говорилось в предыдущей части, служат лишь для контроля верности ввода в таблицу измеренных углов [5].

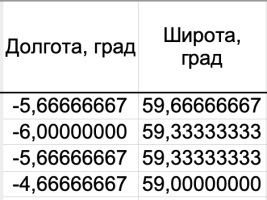
Следующие два столбца, «Долгота» и «Широта» — это как раз те столбцы, куда мы с вами вводим координаты точек пересечения меридиана с параллелью, в которых хотим найти угол касательной к параллели. Еще раз напомню, что этот угол в точности равен углу наклона хорды, которая стягивает два соседних (и равноотстоящих) меридиана. Именно этот второй угол мы и будем измерять и рассчитывать в оставшихся столбцах таблицы.
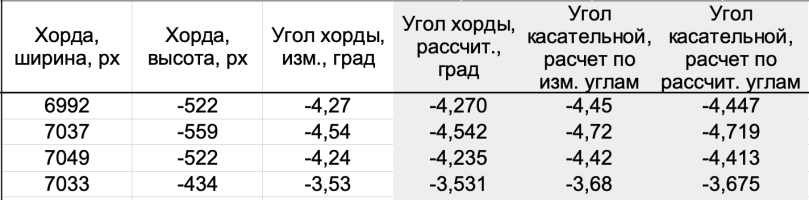
Итак, проведя Измерителем отрезок, стягивающий два меридиана, соседних с интересующим нас, в точках их пересечения с параллелью, получаем три величины: «Хорда, ширина», «Хорда, высота» и «Угол хорды изм.» — точно так же, как и выше при измерении угла наклона рамки. Теперь нам с вами нужно исправить эту измеренную относительно границ растра величину угла на величину угла наклона рамки относительно растра, который мы измерили двумя абзацами выше. Этот расчет и происходит в столбце таблицы «Угол касательной, расчет по изм. углам». Обратите внимание, что для расчета берутся оба угла наклона: верхней и нижней границы рамки и в качестве поправки выступает их усредненная величина. Так следует делать всегда, чтобы уменьшить влияние искажений геометрии листа карты при ее возможной неравномерной деформации.
Что же касается двух столбцов таблицы «Угол хорды, рассчит.» и «Угол касательной, расчет по рассчит. углам» то они точно так же, как и выше для угла наклона сторон рамки носят вспомогательный, контрольный характер и в дальнейших расчетах участия не принимают.
Наконец, в последнем столбце «Примечания» помечены те листы, которые содержали физические дефекты, ошибки или небрежности при сканировании. От них можно было бы ожидать какого-то нестандартного поведения при измерениях или расчетах. Впрочем, исходя из полученных данных, эти опасения, к счастью, не оправдались.
Теперь, прежде чем мы с вами перейдем на следующий лист нашего файла и займемся изучением расчетов, давайте сделаем полшага назад и посмотрим внимательнее, что из себя представляют наши «независимые переменные», которые мы только что обсудили (а именно, «Долгота» и «Широта») и относительно которых мы измеряем переменную зависимую, а именно, угол наклона касательной. Это очень важный вопрос, поскольку относится к плану эксперимента, и его уместнее обсудить прямо сейчас, еще до того, как мы перейдем к расчетам.
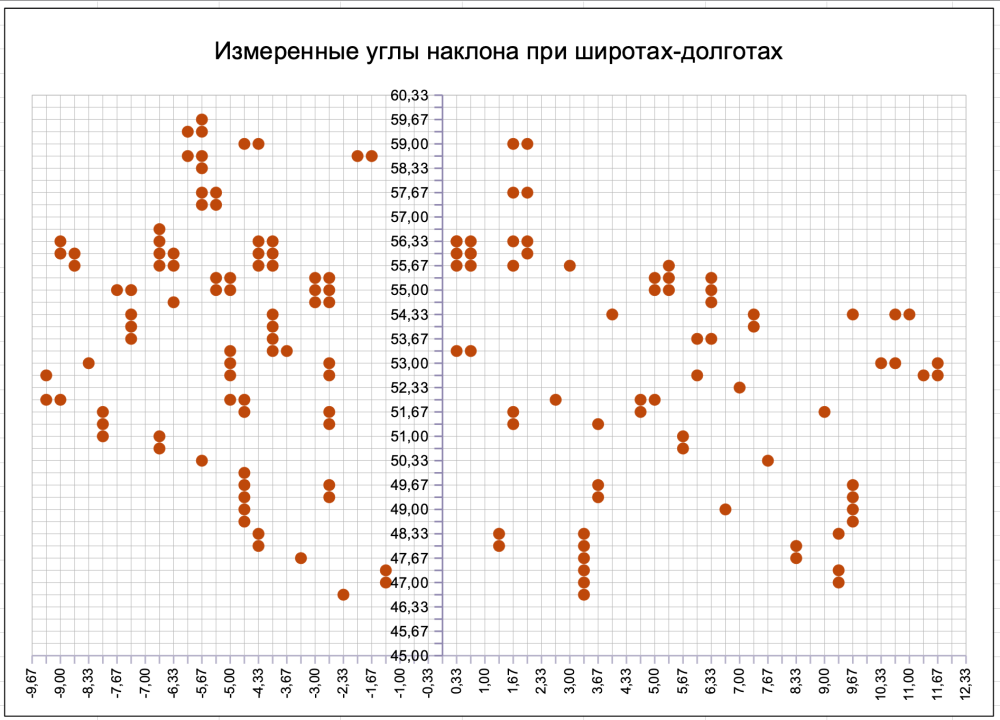
На графике ниже таблицы я отметил точки (в координатах «Широта»-«Долгота») всего массива листов, по которым проведен расчет. Из него легко увидеть, что на самом деле наши «независимые переменные» не так уж независимы [6]! В самом деле, во-первых, они определены не в полностью случайных точках плоскости «Широта»-«Долгота», а лишь только в определенных, с фиксированными значениями. Во-вторых, из-за ограниченности всего набора данных мы даже эти определенные точки не можем выбрать полностью случайно, или хотя бы равномерно, а часто вынуждены пользоваться тем, что есть. И это видно прямо на графике: точки группируются в более или менее регулярную сетку, которая к тому же содержит и регулярные «паттерны» в виде горизонтальных, вертикальных и даже наклонных линий. Такой вид нашего плана заставляет предположить, что мы с вами столкнулись с одной неприятной проблемой статистической обработки таких данных, а именно — с проблемой мультиколлинеарности [7]. Этой проблеме почти всегда отведено место в любом учебнике по статистике, хорошо и доступно она изложена в книге Ф. Картаева [8]. Здесь обсудим ее лишь коротко.
Если говорить простыми словами, то мультиколлинеарность — это наличие сильных связей (корреляций) между «объясняющими» переменными. В пределе такие корреляции могут превращаться в точную функциональную (например, линейную) зависимость. Давайте обсудим, чем это нам может грозить, но прежде для понимания зафиксируем важный факт: эти корреляции могут возникнуть не только из-за того, что переменные на самом деле связаны, скажем, линейной зависимостью, но и из-за того, что мы так выбрали данные для наших с вами расчетов. Именно поэтому я и упомянул «план эксперимента» несколькими абзацами выше.
Итак, сильная мультиколлинеарность приводит к тому, что количество «объясняющих» переменных становится в определенном смысле избыточным. В самом деле, нет никакой необходимости, скажем, в двух объясняющих переменных, если одну можно выразить простой линейной формулой через другую. Говоря в общем и предельном смысле, когда функциональная зависимость между «переменной отклика» и объясняющими переменными неизвестна и лишь моделируется на основе экспериментальных данных это может привести к пересмотру всей модели и исключению из нее какого-то количества переменных. К счастью, это не наш случай: в нашей нелинейной модели мы уверены, а рассчитываем лишь один из параметров этой модели.
Но если мы не должны и не можем менять количество переменных модели, то у нас остается риск, который прямо вытекает из «избыточности» переменных: задача поиска оптимального значения параметра, при котором, например, сумма квадратов отклонений экспериментальных точек от линии нашей нелинейной регресии минимальна, может вообще иметь не единственное решение! Или,что чаще встречается, иметь множество решений в широкой области значений оптимизируемого параметра [9].
Тогда давайте оценим имеющиеся данные. Это делается очень просто: строится таблица (матрица) корреляций значений широты и долготы между собой. В LibreOffice так же как и в Excel для этого есть специальная функция. Эта табличка и приведена под основной таблицей с массивом всех данных. Из нее следует, что на полном массиве из 160 измерений значение коэффициента корреляции между широтой и долготой достигает 0.29 [10]. Много это или мало?

В литературе принято считать, что существенной или «сильной» мультиколлинеарность признается, когда корреляция между «объясняющими» переменными становится больше 0.7. Впрочем, в [8] указана и менее критичная величина: «более 0.9». В то же время диапазон 0.3-0.7 считается областью «средней» мультиколлинеарности. Примерно это значит следующее: у нас нет повода беспокоиться о правильности самой модели, однако вычислительных трудностей здесь можно ожидать.
Так что, исходя из полученной величины корреляции, можно сказать, что на всем массиве данных мы вплотную подобрались к области средней мультиколлинеарности, а поскольку дальнейшее добавление точек эту корреляцию только увеличивает, то на этом количестве есть прямой смысл и остановиться [11]. Еще большим количеством мы не добьемся увеличения точности, а наоборот, можем ее ухудшить за счет худшей сходимости работы алгоритма минимизации.
Дальнейшее обсуждение проблемы мультиколлинеарности выходит за рамки этого цикла; констатируем лишь еще раз, что для дальнейших расчетов нам с вами не требуется больше данных, чем у нас уже есть, и перейдем, наконец, на следующий лист нашего файла: собственно к расчетам.
Полностью текст статьи вы можете прочитать, посетив страницу автора на Boosty.