«Параллель Тучкова». Часть третья, в которой наконец-то становится понятно, почему это важно

Теперь наконец-то подошло время поговорить о том, в чем важность исследования параметров проекции Бонна для трехверстной военно-топографической карты, а именно – широты ее главной параллели. Может быть действительно, речь идет лишь о восстановлении «исторической справедливости» и, как я однажды опрометчиво написал В.Г. Щекотилову, вопрос заключается в «одном-двух пикселях хорошего скана»?

Ответ на этот вопрос, как обычно: «it depends». Или, выражаясь по-русски, «и да, и нет».

Чтобы понять, как так может быть, рассмотрим, как ведет себя проекция Бонна при разных значениях широты главной параллели для всего земного шара. На трех рисунках ниже широта главной параллели возрастает от 0° (этот частный случай проекции называют «синусоидальной») через 45° до 90° (а этот частный случай еще называют «проекцией Вернера»):

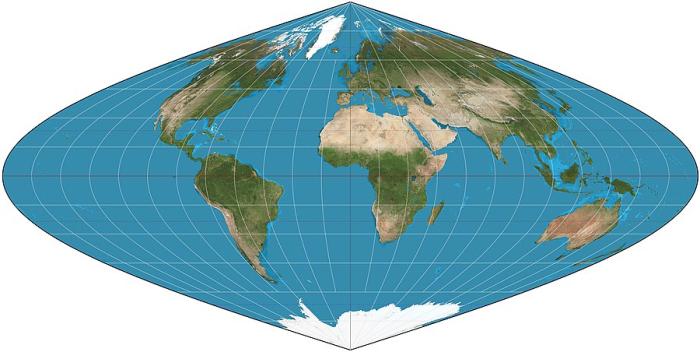
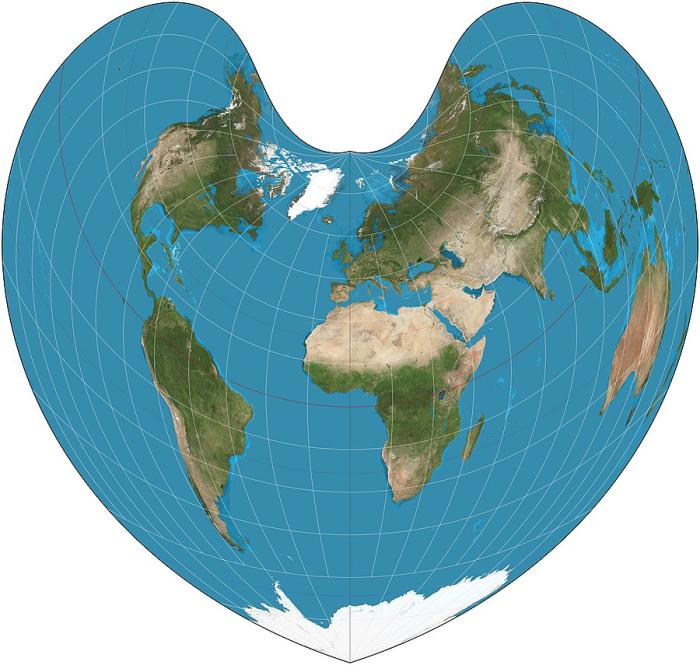
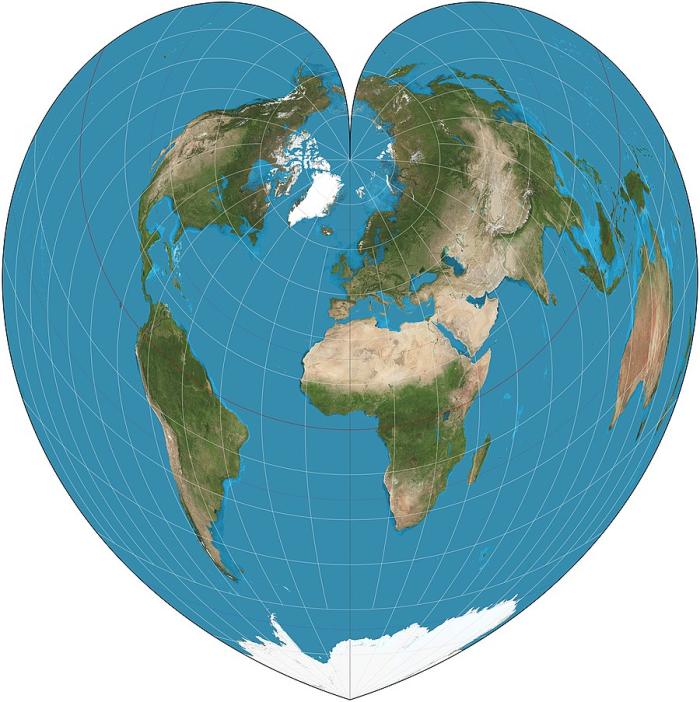
Помимо общего изменения формы проекции от «шлемовидной» до все более «сердцевидной», можно заметить, что изменяется также кривизна параллелей – от прямых линий, перпендикулярных главному меридиану при 0° до окружностей все меньшего радиуса [1].

Для исследуемых нами трехверсток проекция будет выглядеть очень похожей на средний рисунок, с той только разницей, что центральный меридиан у нее не Гринвичский, а Пулковский, и всю картинку континентов следует повернуть вдоль параллелей примерно на 30° в западном направлении. 

А теперь вспомним о том, как выглядит линейная (например, верстовая или километровая) прямоугольная сетка проекции Бонна.

Основные линии сетки образованы непосредственно внутренними рамками каждого листа карты. А каждый лист представляет из себя прямоугольник шириной в 23 и высотой в 16,5 дюймов (69 на 49,5 верст «на местности»). Центральный (Пулковский) меридиан принят за 0° долготы и проходит точно между 8 и 9 вертикальными колоннами разграфки. Один из вариантов такой сетки (параллели и меридианы на нем не показаны) приведен на рисунке ниже.

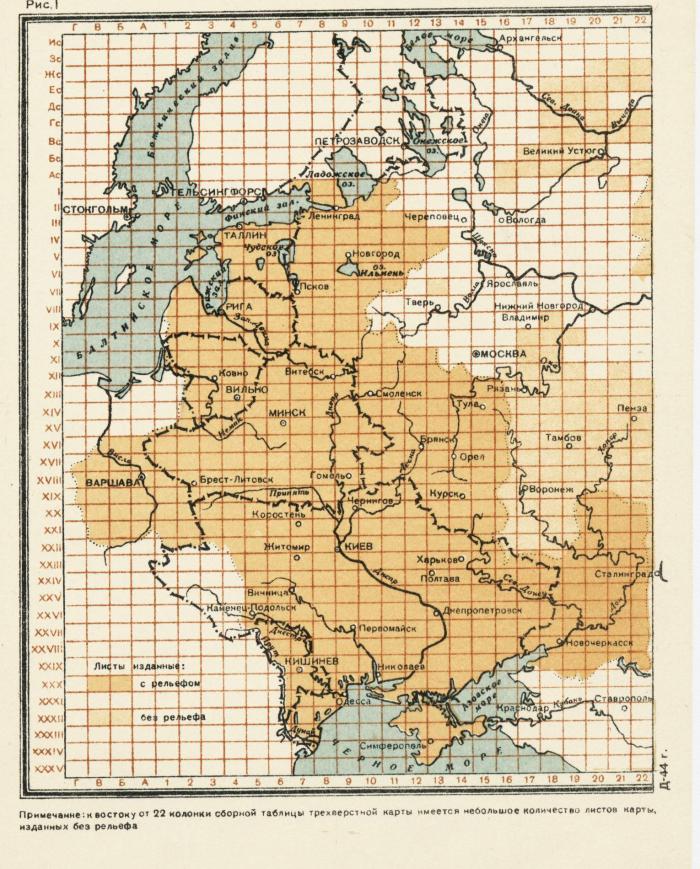
Из того, что 8 и 9 колонны жестко зафиксированы на Пулковском (центральном) меридиане следует, что и все остальные листы зафиксированы «по горизонтали».

Но точно так же сетка зафиксирована относительно центрального меридиана и «по вертикали» и никак не сдвигается при изменении широты главной параллели. Во-первых, начальная точка отсчета линейной сетки проекции Бонна всегда зафиксирована на центральном меридиане (λ(0)) и при некоторой определенной широте φ(0) [2]. А во-вторых, в проекции Бонна масштаб по центральному меридиану в точности равен 1 (а равноотстоящие друг от друга по широте параллели всегда отсекают на центральном меридиане отрезки равной длины) и поэтому все остальные линии всегда занимают одно и то же положение на центральном меридиане независимо от значения широты главной параллели.

Но если на центральном меридиане положение дуг параллелей всегда остается одним и тем же, а линейная сетка представляет собой набор жестких прямоугольников, то очевидно, что при изменении кривизны параллелей (например, увеличении кривизны при увеличении широты главной параллели, как это было показано на рисунках выше) точки пересечения параллелей с вертикальными линиями линейной сетки будут смещаться и этот эффект будет тем сильнее, чем дальше от центрального меридиана находится точка пересечения.

На словах это выглядит замечательно, но как понять количественную сторону эффекта? Для этого можно воспользоваться ранее разработанным калькулятором проекции Бонна для трехверстной карты, в котором есть специальный блок, рассчитывающий линейные координаты точек пересечения границ листов с заданными параллелями.

Такой расчет был проведен в двух вариантах: для листа, непосредственно примыкающего к центральному меридиану (лист XIX-9) и достаточно удаленного [3] от него на восток листа XIX-14. Для каждого из листов был проведен расчет ординаты точки пересечения выбранной «пробной параллели» с правой рамкой карты для разных значений главной параллели (от 52 до 55°). В качестве такой «пробной параллели» была выбрана параллель в 52°, как имеющая приблизительно среднюю кривизну в диапазоне всего покрытия карт.

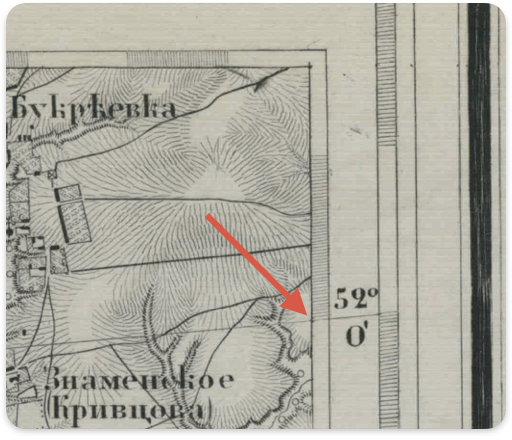
Изобразим то, что мы исследуем, на рисунке. При увеличении широты главной параллели (скажем, от 52 до 55°) обозначенная стрелкой точка пересечения пробной параллели (52°) и рамки карты должна смещаться вверх за счет увеличения кривизны линии (уменьшения ее радиуса):

Полностью текст статьи вы можете прочитать, посетив страницу автора на Boosty.